
Penalaran kuantitatif berhubungan dengan kemampuan berpikir peserta UTBK SNBT 2025 melalui penggunaan angka. Kemampuan berpikir ini melibatkan kuantitas dan hubungan matematika sederhana.
Materi Penalaran Kuantitatif menjadi satu hal yang tidak terlepaskan dari komponen Kemampuan Penalaran umum dalam Tes Potensi Skolastik (TPS). Terdiri 10 soal matematika dasar yang siap menguji peserta UTBK SNBT 2025 dalam waktu 10 menit.
Ada 5 materi matematika dasar yang diujikan dalam bagian ini. Keempatnya yakni operasi bilangan, deret bilangan, perbandingan, persamaan linier, dan data serta penyajiannya.
Agar semakin tergambar, berikut ini 10 contoh soal penalaran kuantitatif yang dikutip dari The King Bedah Tuntas SNBT TPS 2025 karya Forum Tentor Indonesia.
10 Contoh Soal Penalaran Kuantitatif
1.
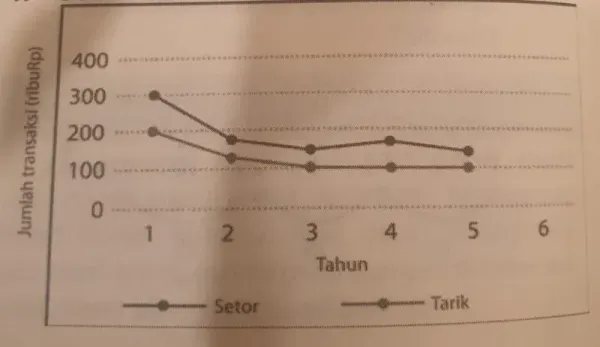
|
Diagram di atas menunjukkan transaksi keuangan berupa penyetoran dan penarikan tabungan seorang karyawan di sebuah bank daerah selama 5 bulan pertama tahun 2021. Berdasarkan data, manakah pernyatan berikut yang PALING TEPAT untuk menggambarkan jumlah transaksi keuangan karyawan tersebut pada bulan ke-6?
A. Jumlah setoran tabungan lebih kecil dibandingkan bulan sebelumnya
C. Jumlah setoran tabungan akan lebih kecil dibandingkan penarikan
D. Jumlah penarikan tabungan lebih kecil dibandingkan bulan sebelumnya
E. Jumlah setoran tabungan sama dengan bulan ketiga
Jawaban: A. Jumlah setoran tabungan lebih kecil dibandingkan bulan sebelumnya
Pembahasan: Berdasarkan diagram pada soal, pernyataan yang PALING TEPAT untuk menggambarkan jumlah transaksi keuangan karyawan pada bulan ke-6 adalah jawaban A. Hal ini dapat dilihat dari grafik setoran yang menurun.
2. Pendapatan A lebih rendah 30% daripada pendapatan B. Berapa pendapatan B jika pendapatan A adalah Rp2.100.000,00?
A. Rp900.000,00
B. Rp1.470.000,00
C. Rp2.370.000,00
E. Rp3.000.000,00
Jawaban: A. Jumlah setoran tabungan lebih kecil dibandingkan bulan sebelumnya
Pembahasan:
Pendapatan A = 70% x Pendapatan B
2.100.000 = 7/100 x Pendapatan B
Pendapatan B = 2.100.000 x 100/7 = 3.000.000
3. Manakah diantara bilangan berikut ini yang nilainya Paling MENDEKATI hasil pengurangan 1,92 - 50/47?
A. 45%
B. 54%
C. 85%
D. 65%
E. 64%
Jawaban: C. 85%
Pembahasan:
Cara 1
1,92 - 50/47 = 1 + 0,92 - 50/47
1,92 - 50/47 = 0,092 - 50/47 + 47/47
1,92 - 50/47 = 0.92 - 3/47
1,92 - 50/47 = 0,92 - 0,0638.....
1,92 - 50/47 = 0,8562.....
1,92 - 50/47 = 85,62...%
Pada pilihan ganda hasil yang mendekati 85,62% adalah 85%.
Cara 2
1,92 - 50/47 = 1,92 - 1,063....
1,92 - 50/47 = 0,856....
1,92 - 50/47 = 85,6...%
Pada pilihan ganda hasil yang paling mendekati 85,6...% adalah 85%
4. Berat angkatan atlet angkat besi pada latihan kesatu sampai kedua secara berturut-turut adalah 98, 107 kilogram, sedangkan pada latihan keempat sampai ketujuh adalah 114, 112, 121, 119 kilogram. Jika tren angkatan tersebut bersifat konstan, berapa kilogram berat angkatan pada latihan ketiga?
A. 105
B. 107
C. 109
D. 113
E. 116
Jawaban: A. 105
Pembahasan: Pada soal terdapat informasi tren berat angkatan bersifat konstan. Sehingga untuk mencari berat angkatan pada latihan ketiga dapat diselesaikan dengan deret bilangan sebagai berikut:
98, 107, ...., 114, 112, 121, 119
98 -> 107: selisih +9
107 -> ....: belum diketahui
.... -> 114: belum diketahui
114 -> 112: selisih -2
112 -> 121: selisih +9
121 -> 119 : selisih -2
Terlihat pola yang terbentuk adalah +9 pertama lalu di jeda angka selanjutnya -2. Sehingga untuk mengetahui yang ketiga adalh 107 - 2 = 105.
Untuk mengetahui betul atau tidak maka, 105 + 9 = 114 (betul). Sehingga jawabannya 105.
5. Hasil perhitungan yang lebih besar dari 7,77 + 5/6 adalah ....
A. 9/12 + 7,75
B. 12/13 + 7,79
C. 13/17 + 7,78
D. 15/19 + 7,76
E. 19/23 + 7,71
Jawaban: B. 12/13 + 7,79
Pembahasan: Untuk menyelesaikan soal tersebut, akan lebih mudah jika diubah dalam bentuk desimal untuk kemudian dibandingkan.
7,77 + 5/6 = 7,77 + 0,833 = 8,603
- Jawaban A diperoleh: 9/12 + 7,75 = 0,75 + 7,75 = 8,5 (lebih kecil)
- Jawaban B diperoleh: 12/13 + 7,79 = 0,92 + 7,79 = 8,71 (lebih besar)
- Jawaban C diperoleh: 13/17 + 7,78 = 0,76 + 7,78 = 8,54 (lebih kecil)
- Jawaban D diperoleh: 15/19 + 7,76 = 0,79 + 7,76 = 8,55 (lebih kecil)
- Jawaban E diperoleh: 19/23 + 7,71 = 0,83 + 7,71 = 8,54 (lebih kecil)
6. Untuk mengecat sebuah dinding dibutuhkan perbandingan cat dan air sebesar 3:1. Jika dinding seluas 600 m^2 membutuhkan 2 liter air, volume cat yang dibutuhkan untuk dinding seluas 2.400 m^2 adalah .....
A. 8 liter
B. 12 liter
C. 16 liter
D. 18 liter
E. 24 liter
Jawaban: E. 24 liter
Pembahasan: Dari perbandingan yang diberikan, dibutuhkan 3 bagian cat untuk 1 bagian air.
Jika 600 m^2 dinding membutuhkan 2 liter air, maka 2.400 m^2 dinding membutuhkan 4 kali lipat air yaitu 8 liter. Sehingga, kita perlu mengalikan 8 liter air dengan 3 untuk mengetahui volume cat yang dibutuhkan. Jawabannya adalah 24 liter car.
7. Jumlah produksi guci dari sebuah pabrik gerabah selama lima hari berturut-turut adalah sebanyak 24, 27, 22, 25, dan 20. Sementara itu jumlah produksi pot pada hari yang sama adalah 13, 9, 11, 7, dan 9. Jika tren dari kedua produksi bersifat konstan, berapa banyak produk guci dan pot pada hari keenam?
A. 15 guci dan 15 buah pot
B. 15 guci dan 13 buah pot
C. 17 guci dan 11 buah pot
D. 23 guci dan 5 buah pot
E. 23 guci dan 13 buah pot
Jawaban: D. 23 guci dan 5 buah pot
Pembahasan: Ada kata kunci bila "kedua produksi bersifat konstan". Sehingga untuk mencari banyak produksi guci dan pot pada hari keenam dapat menggunakan deret bilangan sebagai berikut:
1. Guci
24, 27, 22, 25, 20, .....
Terdapat pola serupa yakni:
24 -> 27: +3
27 -> 22: -5
22 -> 25: +3
25 -> 20: -5
20 -> ....: +3, yakni 20 + 3 = 23
2. Pot
13, 9, 11, 7, 9, .....
Karena bersifat konstan, pot juga memiliki pola yang bisa terlihat yakni:
13 -> 9: -4
9 -> 11: +2
11 -> 7: -4
7 -> 9: +2
9 -> .....: seharusnya -4. Sehingga jumlah yang tepat adalah 9-4 = 5.
8. Setiap hari, A selalu berhasil menjual 18 suvenir yang dibuatnya dengan harga satuan Rp10.000,00. Pendapatan B dari hasil berjualan minuman adalah Rp125.000,00 hingga Rp175.000,00 per hari. Sementara itu, pendapatan C sebagai penjaga toko adalah Rp1.050.000,00 per minggu. Berdasarkan informasi tersebut, manakah pernyataan yang paling tepat mengenai pendapat ketiga orang tersebut?
A. Pendapatan B paling rendah
B. Pendapatan C paling tinggi
C. Pendapatan C lebih besar daripada pendapatan A
D. Pendapatan B lebih besar daripada pendapatan C
E. Pendapatan A dan C tidak mungkin setara
Jawaban: E. Pendapatan A dan C tidak mungkin setara
Pembahasan:
- Pendapatan A per minggu: 18 x 10.000 x 7 = 1.260.000
- Pendapatan B per minggu: (125.000 sampai 175.000) x 7 = 875.000 sampai 1.225.000
- Pendapatan C per minggu: 1.050.000
Dari ketiga orang tersebut, jawaban yang paling tepat adalah E.
9. Karyawan A mendapatkan gaji minimal Rp840.000,00 per minggu. Karyawan B mendapatkan gaji antara Rp110.000,00 hingga Rp125.000,00 per hari, tergantung dari beban kerjanya. Sementara itu, karyawan C mendapatkan penghasilan harian dengan pengangkutan 10 orang per hari, dengan tarif Rp12.000,00 per orang. Jika diasumsikan mereka bekerja 7 hari seminggu, manakah pernyataan yang PALING TEPAT?
A. Gaji karyawan C paling tinggi
B. Gaji karyawan B paling rendah
C. Gaji karyawan A dapat setara dengan gaji karyawan C
D. Gaji karyawan C lebih tinggi daripada karyawan A
E. Gaji karyawan C lebih tinggi daripada karyawan B
Jawaban: C. Gaji karyawan A dapat setara dengan gaji karyawan C
Pembahasan:
- Pendapatan karyawan A per minggu: minimal 840.000
- Pendapatan karyawan B per minggu: (7 x 110.000) 770.000 sampai (7 x 125.000) 875.000
- Pendapatan karyawan C per minggu: 10 x 12.000 x 7 = 840.000
Dari informasi di atas, terlihat bahwa gaji karyawan A dapat setara dengan gaji karyawan C.
10. Jumlah penjualan bunga mawar di sebuah toko selama lima hari berturut-turut adalah 30, 35, 37, 42, dan 44. Sementara itu jumlah penjualan bunga melati untuk lima hari yang sama adalah 13, 14, 16, 19, dan 23. Jika tren penjualan bersifat konstan, berapa jumlah penjualan pada hari keenam?
A. 49 bunga mawar dan 28 bunga melati
B. 49 bunga mawar dan 29 bunga melati
C. 49 bunga mawar dan 30 bunga melati
D. 52 bunga mawar dan 28 bunga melati
E. 42 bunga mawar dan 29 bunga melati
Jawaban: A. 49 bunga mawar dan 28 bunga melati
Pembahasan: Ada kata kunci bila "kedua produksi bersifat konstan". Sehingga untuk mencari banyak penjualan bunga mawar dan bunga melati pada hari keenam dapat menggunakan deret bilangan sebagai berikut:
1. Bunga mawar
30,35,37,42,44,......
Terdapat pola serupa yakni:
30 -> 35: +5
35 -> 37: +2
37 -> 42: +5
42 -> 44: +2
44 -> ....: +5, yakni 44 + 5 = 49
2. Bunga melati
13, 14, 16, 19, 23, .....
Karena bersifat konstan, bunga melati juga memiliki pola yang bisa terlihat yakni:
13 -> 14: +1
14 -> 16: +2
16 -> 19: +3
19 -> 23: +4
23 -> .....: seharusnya +5. Sehingga jumlah yang terpat adalah 23+5 = 28.
Itulah 10 contoh soal tentang penalaran kuantitatif. Terus berlatih ya detikers!









